Spatial Distribution of Magnetic Field Under Spherical Shell Plasma
Xinhua Song,
Honghao Yan,
Zhengzheng Ma,
Yang Wang and
Bing Xu
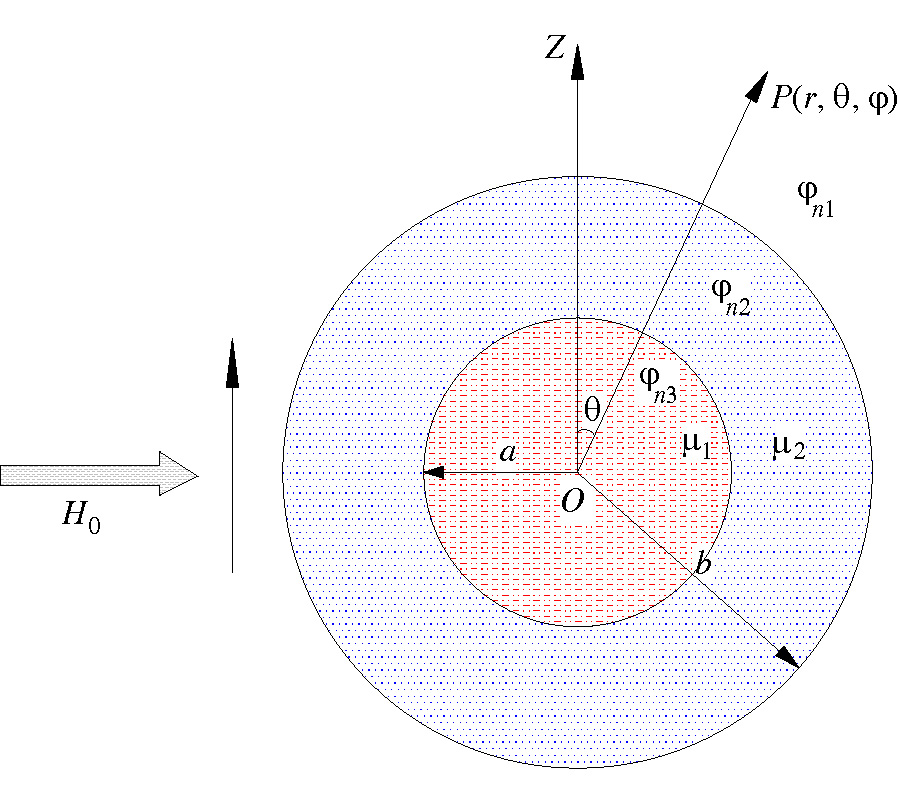
Magnetic field intensity is modeled using Laplacian equations to study the spatial distribution of magnetic field under spherical shell plasma. The influences of different internal and external radii are also considered. In addition, the magnetic field calculation of plasma space is analyzed. The main conclusions are as follows. The external uniform magnetic field H0 is the scalar magnetic bit, and the magnetic charge of the shell of the plasma is equivalent to that of a magnetic dipole. The magnetic field in the spherical shell is a super position of a uniform field and a magnetic dipole field. The uniform field is composed of an externally applied uniform field H0 and a uniform field generated by the magnetic charge on the outer surface of the ball. The magnetic dipole field is generated by the magnetic charge on the inner surface of the shell, and the inside of the shell is a uniform magnetic field. When μ2/μ1 is high and a/b is low, the ratio of the magnetic field strength H3 (the regionis r<a) to the magnetic field strength H0 (the region is r>b) is low. By contrast, when μ2/μ1 and a/b are high, the ratio of the magnetic field strength H3 to the magnetic field strength H0 is high. When the magnetic permeability of the inner object is small and the spherical shell is thick, the produced plasma sheath is thick, and the external magnetic field in the spherical shell is weak. Therefore, when the shielding effect is good, the possibility that the ``black barrier'' phenomenon will occur is high, and ground radar detection will be difficult.