PIER M | PIER Journals

2013-05-08

PIER M

Vol. 30, 253-269, 2013

download: 681

Modeling of the Direct Lightning Strike on a Towers Cascade Equipped with Its Protections

Lotfi Boufenneche, Bachir Nekhoul, Kamal Kerroum, Khalil El Khamlichi Drissi and Dragan Poljak

In this paper, a direct time domain approach based on the corresponding transmission lines equations and Finite Difference Time Domain (FDTD) method is proposed to analyze a direct lightning strike to a cascade of transmission line towers. The proposed model deals with a real case of towers being connected by ground wires and equipped with grounding systems with different topologies, as well(vertical or horizontal conductor buried in the ground, crow's feet in the ground...). In particular, this work realistically represents the tower geometry and accounts for the propagation phenomena along the tower and between the towers. The proposed direct time domain approach deals with rather complex electrical devices (towers, ground wires and grounding systems), but at the same time requires very low computational cost and also provides relatively simple implementation. Some illustrative computational examples related to some engineering applications are given in the paper.

MODELING OF THE DIRECT LIGHTNING STRIKE ON A TOWERS CASCADE EQUIPPED WITH ITS PROTECTIONS

2013-05-08

PIER M

Vol. 30, 239-252, 2013

doi:10.2528/PIERM13022512

download: 619

Collocated Sibc-FDTD Method for Coated Conductors at Oblique Incidence

Lijuan Shi, Lixia Yang, Hui Ma and Jianning Ding

A collocated surface impedance boundary condition (SIBC)-finite difference time domain (FDTD) method is developed for conductors coated with lossy dielectric coatings at oblique incidence. The method is based on the collocated electric and magnetic field components on the planar interface between two media, and rational approximation for tangent function of surface impedance formulation is adopted. In contrast to the traditional SIBC-FDTD implementation which is approximated with the magnetic field component on the boundary located at half-cell distance from the interface and half time step earlier in time, the collocation approach is more accurate for both magnitude and phase of reflection coefficient. By the comparison with exact results, the proposed model is numerically verified in the frequency domain for both parallel polarization plane wave and vertical polarization plane wave at varying oblique angles of incidence.

COLLOCATED SIBC-FDTD METHOD FOR COATED CONDUCTORS AT OBLIQUE INCIDENCE

2013-05-07

PIER M

Vol. 30, 225-238, 2013

doi:10.2528/PIERM13032105

download: 573

An Analytic Expression for Near-Field Angular Glint Prediction of Radar Sensor Using Far-Field Scattering Centers Models

Jianpeng Fan, Shijie Fan, Hongqi Fan and Huaitie Xiao

As an important signature of the radar target, the angular glints effects on radar sensor mainly arise at close distance, especially at target near field. However, the current prediction methods of angular glint are mostly based on the far field condition. This paper presents a prediction technique of near field angular glint based on the scattering center model to solve this problem. Firstly, the near field backscattering is represented based on far-field scattering center model. Then by solving the derivative of the backscattering phase vs. the position vector of the observer, including incident angles and range, we get the exact expression of angular glint at near field. Next, the exact expression is approximated and simplified in the range of terminal guidance. Finally, the factors affecting near-field angular glint are analyzed using numeric simulation, and the error comparison between the exact and approximate expression is also provided. It is concluded that the expression in [1] is the approximation of ours at far field under certain polarization, and the simplified expression has a well precision in the range of terminal guidance. All these results provide the theoretical basis for the prediction of near field angular glint and its signature research.

AN ANALYTIC EXPRESSION FOR NEAR-FIELD ANGULAR GLINT PREDICTION OF RADAR SENSOR USING FAR-FIELD SCATTERING CENTERS MODELS

2013-04-27

PIER M

Vol. 30, 211-224, 2013

doi:10.2528/PIERM12122406

download: 546

A Support Vector Machine for Identification of Monitors Based on Their Unintended Electromagnetic Emanation

Fan Mo, Ying-Hua Lu, Jinling Zhang, Qiang Cui and Sihai Qiu

Electrical equipments usually radiate unintended emission which carries characteristic information when running, such as emanation from computers monitors, keyboards and other components, this emanation can be possibly used to reconstruct the source information. Most of the experiments related to this area are carried out inside a semi-anechoic chamber, and measurement out of it may not be considered to be optimal, because the data captured are usually not sufficient. Yet in this study, we take LCD monitors as typical examples and find that characteristics significantly differ between products, parameters such as the magnitude and spectrum were measured under normal environment. We take the PCB traces as antennas and acquire the raw signal directly near the antenna and extract the parameters to use as input to support vector machine (SVM) which was trained to identify the emanating source(LCD monitors). In this study, the method was tested using the emission captured from one Samsung (SyncMaster E1920) and two LG (L1753s) monitors, and a laptop(ACER Aspire 5542). The SVM was able to classify the source of signals with 98.9510% accuracy while using emission that captured from the running monitors.

A SUPPORT VECTOR MACHINE FOR IDENTIFICATION OF MONITORS BASED ON THEIR UNINTENDED ELECTROMAGNETIC EMANATION

2013-04-25

PIER M

Vol. 30, 195-209, 2013

doi:10.2528/PIERM13032006

download: 1069

Stub Based Equivalent Circuit Models for Even/Odd Mode Dual CRLH Unit Cells

Amr M. E. Safwat, Amr A. Ibrahim, Mohamed A. Othman, Marwah Shafee and Tamer Mostafa Abuelfadl

The theory of even/odd mode based dual composite right/left handed (D-CRLH) unit cells is developed, and a unified modeling approach based on stubs is presented. The theory shows that these unit cells will have left-handed behavior if the even and odd mode corresponding stubs have dual behavior. Several unit cells are investigated. The proposed models agree with EM simulations. Experimental results confirm the presented theory.

STUB BASED EQUIVALENT CIRCUIT MODELS FOR EVEN/ODD MODE DUAL CRLH UNIT CELLS

2013-04-18

PIER M

Vol. 30, 183-194, 2013

doi:10.2528/PIERM13022602

download: 641

Retrieving Evaporation Duct Heights from Power of Ground-Based GPS Occultation Signal

Hong-Guang Wang, Zhen-Sen Wu, Leke Lin, Shi-Feng Kang and Zhenwei Zhao

Evaporation duct is a manifest phenomenon that can affect microwave propagation seriously with low elevation angles near the sea surface. As an important parameter to describe the characteristic of the evaporation duct, duct height can be estimated from radar sea echo using a technique called as "refractivity from clutter". In this study, we proposed a novel approach to estimating the evaporation duct height. The signal power received by a ground-based GPS receiver is used when the GPS satellites rise or set at the local horizon over the sea. A forward propagation model and genetic algorithm are adopted to implement this method. The performance is evaluated via numerical simulation for inferring evaporation duct with different height. The results showed that the proposed method is well effective, especially for the conditions with higher evaporation duct height.

RETRIEVING EVAPORATION DUCT HEIGHTS FROM POWER OF GROUND-BASED GPS OCCULTATION SIGNAL

2013-04-18

PIER M

Vol. 30, 167-181, 2013

doi:10.2528/PIERM13032110

download: 1469

Analytical Investigation of Periodic Coplanar Waveguides

Teng-Kai Chen and Gregory H. Huff

This paper presents an analytical formula to evaluate even- and odd-mode characteristics of infinitely parallel coplanar waveguides (CPW) with the same dimensions in each CPW, given name as periodic coplanar waveguides (PCPW). The analysis yields a closed-form expression based on the quasi-TEM assumption and conformal mapping transformation. Calculated results show that both the even- and odd-mode characteristic impedances are in good agreements with the results generated by numerical solvers and available experimental data. The results are important especially for highly demand on miniaturization of circuit design to place multiple CPWs in parallel.

ANALYTICAL INVESTIGATION OF PERIODIC COPLANAR WAVEGUIDES

2013-04-18

PIER M

Vol. 30, 153-165, 2013

doi:10.2528/PIERM12123007

download: 682

Scintillation Index of a Gaussian Schell-Model Beam on Slant Atmospheric Turbulence

Ning-Jing Xiang and Zhen-Sen Wu

Based on the altitude-dependent model of the ITU-R slant atmospheric turbulence structure constant model, we present scintillation index calculations for a partially coherent Gaussian Schell-model (GSM) beam under all irradiance fluctuation conditions. The longitudinal and radial components of the scintillation index are treated separately. Our results correctly reduce to the result of the horizontal path with atmospheric structure constant fixed; and simplify to a fully coherent Gaussian beam with source coherence parameter ζ representing unit. The numerical conclusions indicate that within specific source and parameter ranges, a partially coherent GSM beam is capable of offering less scintillation in comparison with the full coherent Gaussian beam. Before the maximum value of the scintillation, the scintillation index of the partially coherent GSM beam will decrease with the increased altitude. However the off axis radial scintillation index will vanish when the Rytov variance is infinity.

SCINTILLATION INDEX OF A GAUSSIAN SCHELL-MODEL BEAM ON SLANT ATMOSPHERIC TURBULENCE

2013-04-17

PIER M

Vol. 30, 141-152, 2013

doi:10.2528/PIERM13020706

download: 635

Design of Metaparticles as Sharp Frequency-Selective Obscurant Aerosols

Sharhabeel Alyones, Al. V. Jelinek, Michael Granado and Charles W. Bruce

In this article, artificial aerosol metaparticles are investigated. These particles are based on interacting single split rectangular resonators (SRRs) imprinted on a one-sided thin dielectric substrate. These particles produce sharper transmission bandstops with adjustable bandwidths compared to conventional artificial aerosol obscurants like fibers, spheres, discs. The particle design is performed in the microwave region with the intention to be scalable to the infrared. Particles with couplings between two, three, and four SRRs are introduced. Numerical simulations and experimental measurements of the transmission parameter of the particles are introduced and compared with fibrous aerosols. These particles may be used as good electromagnetic obscurants in the atmosphere.

DESIGN OF METAPARTICLES AS SHARP FREQUENCY-SELECTIVE OBSCURANT AEROSOLS

2013-04-17

PIER M

Vol. 30, 129-139, 2013

doi:10.2528/PIERM13030607

download: 580

Theoretical and Experimental Studies of Magnetic Field on Electromagnetic Wave Propagation in Plasma

Xiaojun Xing, Qing Zhao and Ling Zheng

A spacecraft will experience the well-known ``blackout'' problem in the re-entry into the Earth's atmosphere, which results in communication failures between the spacecraft and ground control center. It is important to study the blackout mitigation method. The effects of external magnetic field on electromagnetic wave propagation in plasma are studied by theoretical and experimental methods in this paper. The numerical results show that the attenuation of electromagnetic wave in plasma is reduced by the presence of a magnetized field. The propagation properties of electromagnetic wave in unmagnetized and magnetized plasma have been studied experimentally with plasma torch, and the experimental results are in good agreement with the theory. Both the theoretical and experimental results indicate that magnetic window is an alternative and promising way to improve the radio blackout issue.

THEORETICAL AND EXPERIMENTAL STUDIES OF MAGNETIC FIELD ON ELECTROMAGNETIC WAVE PROPAGATION IN PLASMA

2013-04-12

PIER M

Vol. 30, 117-128, 2013

doi:10.2528/PIERM12121503

download: 611

Multi-Output Least Square Support Vector Machine for the Reconstruction of Perfect Electric Conductor Below Rough Surface

Ji-Liang Cai, Chuang-Ming Tong and Wei-Jie Ji

To save the computation time and improve the accuracy of reconstruction results by support vector machine (SVM), a multi-output least square SVM (LS-SVM) algorithm is proposed to reconstruct the position of a 2-D perfect electric conductor cylinder below a rough surface. Firstly, the scattered electromagnetic field at a number of observation positions is calculated by the method of moment to generate the training and testing data. Then the multi-output LS-SVM is trained to reconstruct the coordinate of the object center. Numerical results show that this approach is accurate and efficient even with some additive Gaussian noise.

MULTI-OUTPUT LEAST SQUARE SUPPORT VECTOR MACHINE FOR THE RECONSTRUCTION OF PERFECT ELECTRIC CONDUCTOR BELOW ROUGH SURFACE

2013-04-11

PIER M

Vol. 30, 105-116, 2013

doi:10.2528/PIERM13020504

download: 562

A Way to Improve the Accuracy of Displacement Measurement by a Two-Probe Implementation of Microwave Interferometry

Aleksei V. Doronin, Nikolai B. Gorev, Inna F. Kodzhespirova and Evgeny N. Privalov

This paper addresses the possibility of displacement measurement by microwave interferometry at an unknown reflection coefficient with the use of as few as two probes. The case of an arbitrary interpobe distance is considered. The measurement error as a function of the interprobe distance is analyzed with the inclusion of variations of the detector currents from their theoretical values. The analysis has shown that as the interprobe distance decreases, the maximum measurement error passes through a minimum for reflection coefficients close to unity and increases monotonically for smaller reflection coefficients. Based on the results of the analysis, the interprobe distance is suggested to be one tenth of the guided operating wavelength λ_g. In comparison with the conventional interprobe distance of λ_g/8, the suggested one offers a marked reduction in the maximum measurement error for reflection coefficients close to unity, while for smaller ones this error remains much the same (for a detector current error of 3%, the maximum measurement error in percent of the operating wavelength is 2.2% and 1.0% at λ_g/10 as against 4.8% and 2.7% at λ_g/8 for a reflection coefficient of 1 and 0.9, respectively, and 2.9% at λ_g/10 as against 2.4% at λ_g/8 for a reflection coefficient of 0.1).

A WAY TO IMPROVE THE ACCURACY OF DISPLACEMENT MEASUREMENT BY A TWO-PROBE IMPLEMENTATION OF MICROWAVE INTERFEROMETRY

2013-04-10

PIER M

Vol. 30, 95-104, 2013

doi:10.2528/PIERM13030402

download: 487

Using Spherical Shells for Gain Enhancement of Compact Wideband Phased Arrays

Abdelnasser Eldek

Spherical shells are proposed and presented to improve the gain of a class of wideband phased array systems. This kind of phased arrays is composed of compact elements, which allow for a small distance between elements that is much less than half wavelength at lower operating frequencies. This small distance, as a function of wavelength, results in a small gain. Therefore, shells confronting the array are proposed to improve the gain. The formulations required to define the geometry and material properties of the shell are developed. Two and four element arrays are designed and simulated with and without shells to test the technique, and promising results are obtained at lower frequencies for the array with shells.

USING SPHERICAL SHELLS FOR GAIN ENHANCEMENT OF COMPACT WIDEBAND PHASED ARRAYS

2013-04-09

PIER M

Vol. 30, 79-93, 2013

doi:10.2528/PIERM12101504

download: 625

An Exact Formulation for the Reflection Coefficient from Anisotropic Multilayer Structures with Arbitrary Backing

Maryam Heidary, Ali Abdolali and Mohammad Mahdi Salary

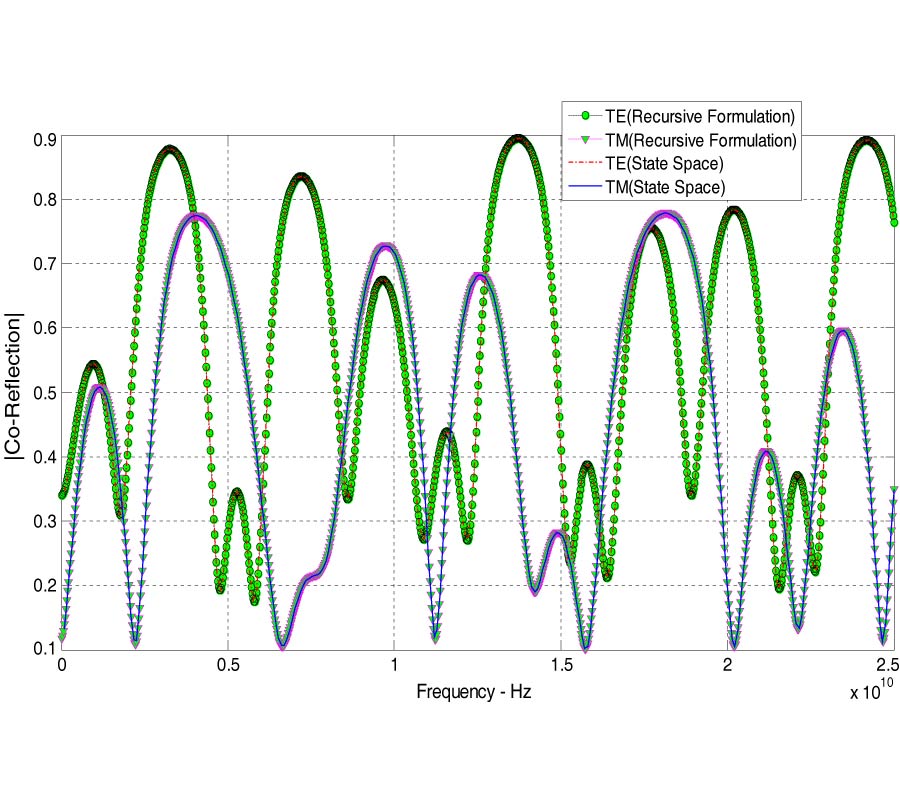
This paper is concerned with the theory of wave propagation in biaxial anisotropic media. Consider a multilayered planar structure composed of media with electric and magnetic anisotropy, surrounded by two half spaces. Exat relations for reflection coefficient from this structure can be useful for arriving at the intended applications. In this paper, by matching of transverse field components at the bounderies, we will arrive at exact recursive relations for reflection coefficient of the structure. In the previous works, the magnetic and electric anisotropy were not taken into consideration at the same time, or complex relations were arrived. But using this novel method, those complexities will not appear and both electric and magnetic anisotropy are take into consideration. Moreover, we will not set any limits on the right half-space so the right most half-space may be a PEC, PMC, PEMC, surface impedance, dielectric or a metamaterial. Finally, the last section of the paper confirms the validity of the relations arrived at and as an interesting application; the zero reflection condition will be obtained.

AN EXACT FORMULATION FOR THE REFLECTION COEFFICIENT FROM ANISOTROPIC MULTILAYER STRUCTURES WITH ARBITRARY BACKING

2013-03-27

PIER M

Vol. 30, 67-77, 2013

doi:10.2528/PIERM13012816

download: 473

The Adi-FDTD Method Including Lumped Networks Using Piecewise Linear Recursive Convolution Technique

Fen Xia, Qing-Xin Chu, Yong-Dan Kong and Zhi-Yong Kang

The lumped network alternating direction implicit finite difference time domain (LN-ADI-FDTD) technique is proposed as an extension of the conventional ADI-FDTD method in this paper, which allows the lumped networks to be inserted into some ADI-FDTD cells. Based on the piecewise linear recursive convolution (PLRC) technique, the current expression of the loaded place can be obtained. Then, substituting the expression into the ADI-FDTD formulas, the difference equations including an arbitrary linear network are derived. For the sake of showing the validity of the proposed scheme, lumped networks are placed on the microstrip and the voltage across the road is computed by the lumped network finite difference time domain (LN-FDTD) method and LN-ADI-FDTD method, respectively. Moreover, the results are compared with those of obtained by using the circuital simulator ADS. The agreement among all the simulated results is achieved, and the extended ADI-FDTD method has been shown to overcome the Courant-Friedrichs-Lewy (CFL) condition.

THE ADI-FDTD METHOD INCLUDING LUMPED NETWORKS USING PIECEWISE LINEAR RECURSIVE CONVOLUTION TECHNIQUE

2013-03-21

PIER M

Vol. 30, 51-66, 2013

doi:10.2528/PIERM13012207

download: 722

Thermo-Mechanical Analysis of an Improved Thermal through Silicon via (Ttsv) Structure

Lin-Juan Huang and Wen-Sheng Zhao

Temperature and thermal stress responses of an improved TTSV structure under the impact of hotspots are numerically analyzed in this paper. A Fin structure is added to the circular TTSV to strengthen the effect of thermo-mechanical mitigation. The nonlinear finite element method (N-FEM) is presented to obtain the coupled thermal and mechanical fields. Running time of the N-FEM algorithm is compared with that of commercial software to indicate its efficiency. The model of state-of-the-art 3D Dynamic Random Access Memory (DRAM) is adopted in our simulation. Besides the single-layer TTSV and TTSV array, the extended case of multi-layer TTSVs is also investigated. To take into consideration the nonlinear effects, the temperature dependent results for the issues of hotspot alignment and liner materials selection are provided, both of which are compared with the corresponding temperature independent results. This paper is aimed to provide some practical guidance to the design of TTSV for effective thermo-mechanical management.

THERMO-MECHANICAL ANALYSIS OF AN IMPROVED THERMAL THROUGH SILICON VIA (TTSV) STRUCTURE

2013-03-19

PIER M

Vol. 30, 39-50, 2013

doi:10.2528/PIERM13011403

download: 500

A Dual-Band Terahertz Metamaterial Based on a Hybrid 'h'-Shaped Cell

Wanyi Guo, Lianxing He, Hao Sun, Hongwei Zhao, Biao Li and Xiao-Wei Sun

We present a dualband terahertz metamaterial based on a hybrid 'H'-shaped cell of different sizes. The proposed 'H'-shaped metamaterial (HSM) structure, fabricated on a quartz (SiO₂) substrate, exhibits two intense electrical resonances at ~0.95 THz and ~1.26 THz, respectively. Extracted effective permittivity show negative values in 0.95-1.01 THz and 1.26-1.42 THz bands. Measured results from the terahertz time-domain spectroscopy (THz-TDS) experiments show good agreement with the simulated results.

2013-03-18

PIER M

Vol. 30, 25-37, 2013

doi:10.2528/PIERM13012201

download: 869

A Fast Tuning Method for Microwave Filter Using VF-Asm Technology

Yong-Liang Zhang, Tao Su, Zhi-Peng Li and Chang-Hong Liang

A novel microwave filter tuning method based on vector fitting and aggressive space mapping (VF-ASM) technology is presented in this paper. The filter tuning is performed as a two step procedure. First, the equivalent circuit parameters are extracted through vector fitting method by a series of S-parameter measurements. Second, the optimal screw positions are calculated through ASM techniques. this novel tuning technique has been tested successfully with cross-coupled six-resonator and direct coupled eight-resonator filters.

A FAST TUNING METHOD FOR MICROWAVE FILTER USING VF-ASM TECHNOLOGY

2013-03-17

PIER M

Vol. 30, 11-23, 2013

doi:10.2528/PIERM12110609

download: 1409

Electromagnetic Wave Propagation in Soil for Wireless Underground Sensor Networks

Xiaoqing Yu, Pute Wu, Zenglin Zhang, Ning Wang and Wenting Han

Wireless underground sensor networks (WUSN) consist of wireless devices that operate below the ground surface. These devices are buried completely under dense soil, thus electromagnetic wave transmits only through soil medium. However, the high attenuation that caused by soil is the main challenge for the electromagnetic wave transmission for WUSN. In this study, architecture of wireless underground sensor network communication was established. The experimental measurements were conducted using WUSN sensor nodes at three different carrier frequencies, respectively. Received signal strength and packet error rate were examined for communication links between the sensor nodes. The test results showed that carrier frequency was one of the main factors that affected electromagnetic wave propagation in the soil medium. It was concluded that the burial depth of the sensor nodes, horizontal inter-node distance, and soil volumetric water content have significant impacts on the signal strength and packet error rate during the electromagnetic wave propagation within a WUSN.

ELECTROMAGNETIC WAVE PROPAGATION IN SOIL FOR WIRELESS UNDERGROUND SENSOR NETWORKS

2013-03-17

PIER M

Vol. 30, 1-10, 2013

doi:10.2528/PIERM13022803

download: 829

Materials Insertion Loss at 2.4, 3.3 and 5.5 GHz Bands

Bazil Taha-Ahmed, Ignacio Alvarez Calvo and Jose Luis Masa-Campos

The insertion loss of different materials is measured at 2.4, 3.3 and 5.5 GHz bands. Directive antennas with a nominal gain of 19 dB are used in the measurement campaign. The height of the antennas has been selected to have the minimum possible reflection from around surfaces. Metallic door with porthole window, metallic grid, glass window, human beings and tree's insertion loss are measured. The metallic grid presents a band pass filter function with a resonance frequency between 3.2 to 3.3 GHz. Other materials have an insertion loss that increases with the increment of the operating frequency.