Formulating a Vector Wave Expression for Polarimetric GNSS Surface Scattering
Robert N. Treuhaft,
Stephen T. Lowe and
Estel Cardellach
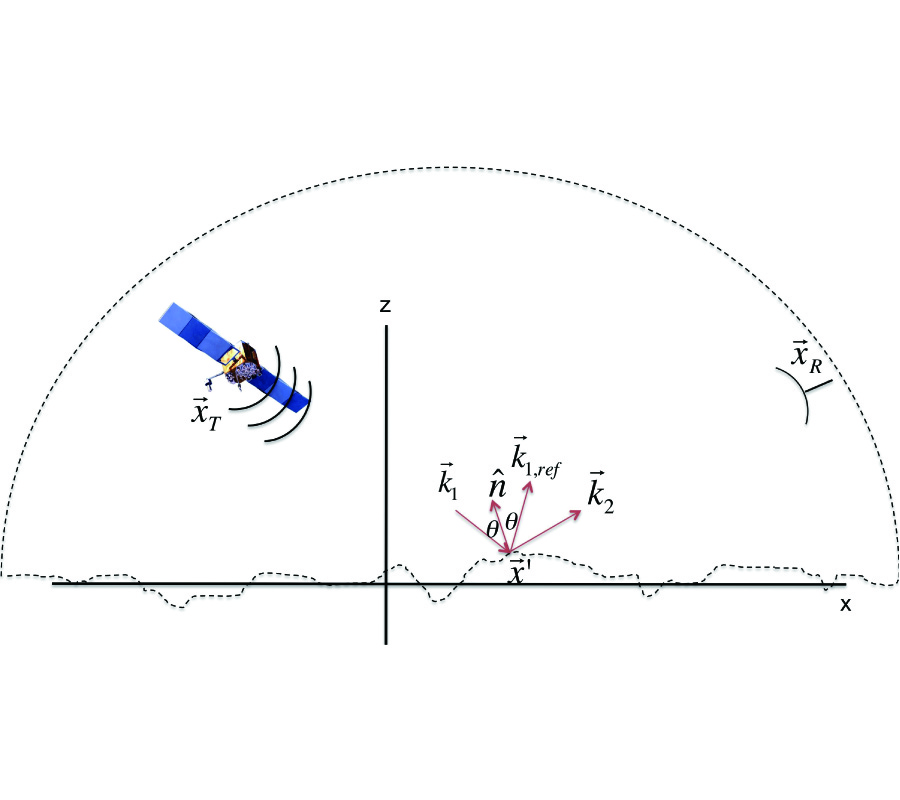
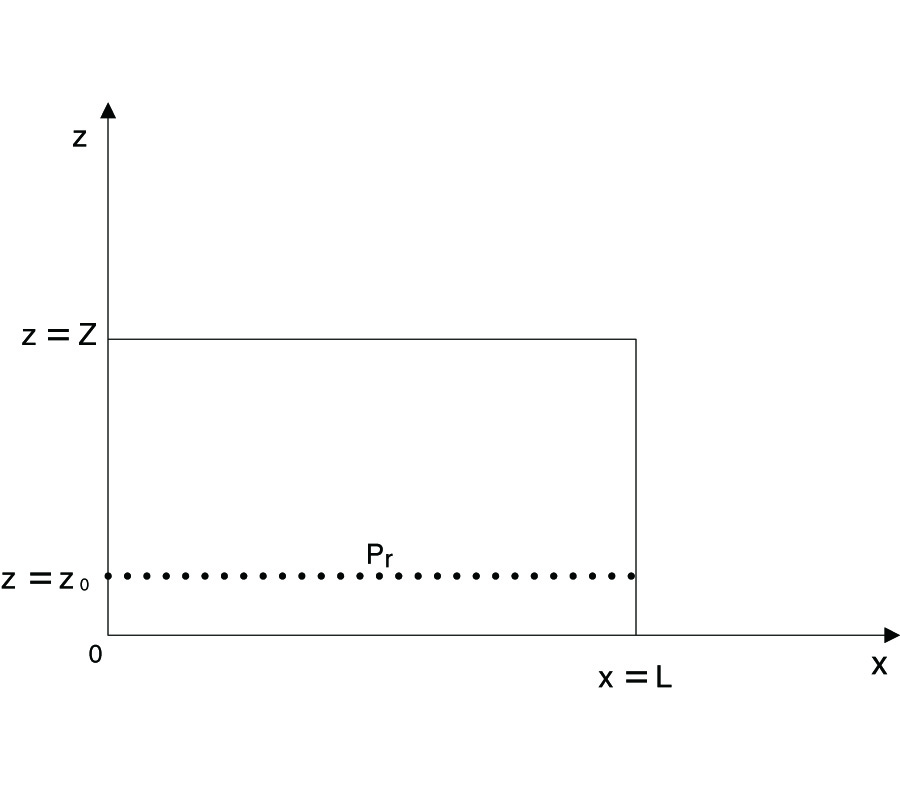
This paper formulates a simple vector integral expression for electromagnetic waves received after scattering from a surface. The derived expression is an alternative to the Stratton-Chu equation frequently used for polarimetric surface scattering. It is intended for use in polarimetric Global Navigation Satellite System (GNSS) ocean remote sensing, or any type of polarimetric remote sensing from surfaces, when the surface roughness pattern is known from simulation or data. This paper is intended to present a complete accounting of the steps leading to the simpler vector integral expression. It therefore starts with the scalar case, using Maxwell's equations and Green's theorem. It principally treats the case of a transmitter within the integration volume, but discusses how the formalism changes if the transmitter is outside of the integration volume, as with plane waves. It then shows how the scalar expression can be extended to a vector expression for the component of the electric field in an arbitrary receive-polarization direction due to scattering from a rough surface of an incident wave with an arbitrary transmit polarization. It uses the Kirchhoff, or tangent-plane, approximation in which each facet on the ocean is considered to specularly reflect the incoming signal. The derived vector expression is very similar to that for a scalar wave, but it includes all vector properties of the scattering. Equivalence is demonstrated between the Stratton-Chu equation and the derived, simpler expression, which is operationally easier to code than the Stratton-Chu equation in many modeling applications.