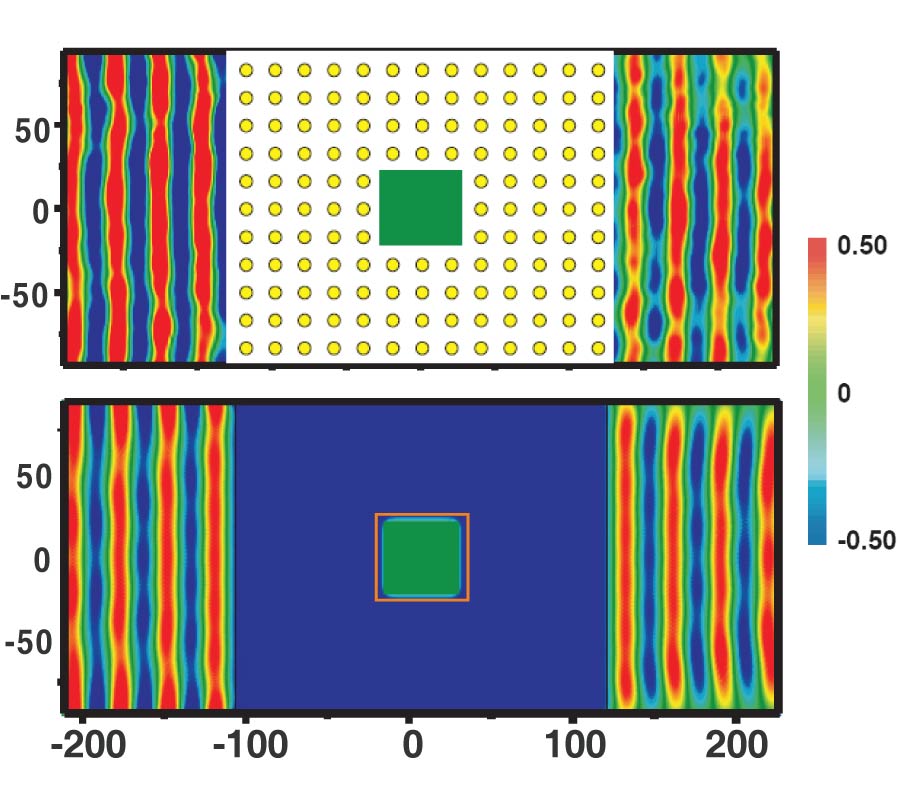
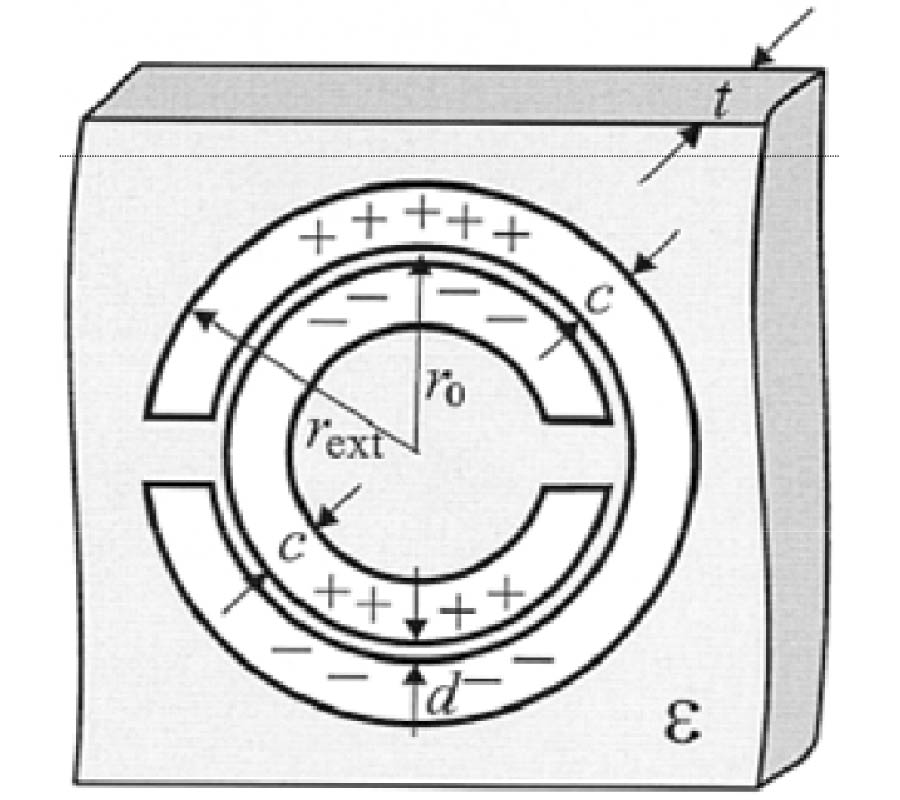
Dirac Dispersion and Zero-Index in Two Dimensional and Three Dimensional Photonic and Phononic Systems (Invited Paper)
Che-Ting Chan,
Xueqin Huang,
Fengming Liu and
Zhi Hong Hang
We show that by applying accidental degeneracy, we can obtain a triply-degenerate state at the zone center in the band diagram of two dimensional (2D) photonic crystal. The dispersion near the zone center comprisestwo linear bands and an additional flat band crossing at the same frequency. If this triply-degenerate state is formed by the degeneracy of monopole and dipole excitations, we show that the system can be mapped to an effective medium with permittivity and permeability equal to zero.While "Dirac cone" dispersions can only be meaningfully defined in 2D systems, the notion of a Dirac point can be extended to three dimensional (3D) classical wave systems. We show that a simple cubic photonic crystal composed of core-shell spheres exhibitsa 3D Dirac-like point at the center ofthe Brillouin zone at a finite frequency. Using effective medium theory, we can map our structure to an isotropiczero refractive index material inwhich the effective permittivity and permeability are simultaneously zero at the Dirac-like point frequency (ωD). The Dirac-like point is six-fold degenerate and is formed by the accidental degeneracy of electric dipole and magnetic dipole excitations, each with three degrees of freedom. We found that 3D Dirac-like pointsat can also be found in simple cubic acoustic wave crystals.Different from the case in the photonic system,the 3D Dirac-like points at \overrightarrow{k}= 0 in acoustic wave systemis four-fold degenerate, and is formed by the accidental degeneracy of dipole and monopole excitations. Using effective medium theory, this acoustic wave system can also be described as a materialwhich hasboth effective mass density and reciprocal of bulk modulus equal to zero at ωD. For both the photonic and phononic systems, a subset of the bands has linear dispersions near the zone center, and they give rise to equi-frequency surfaces that are spheres with radii proportional to (ω - ωD).