Dielectric Wedge Scattering: an Analytic Inroad
Jan Alexander Grzesik
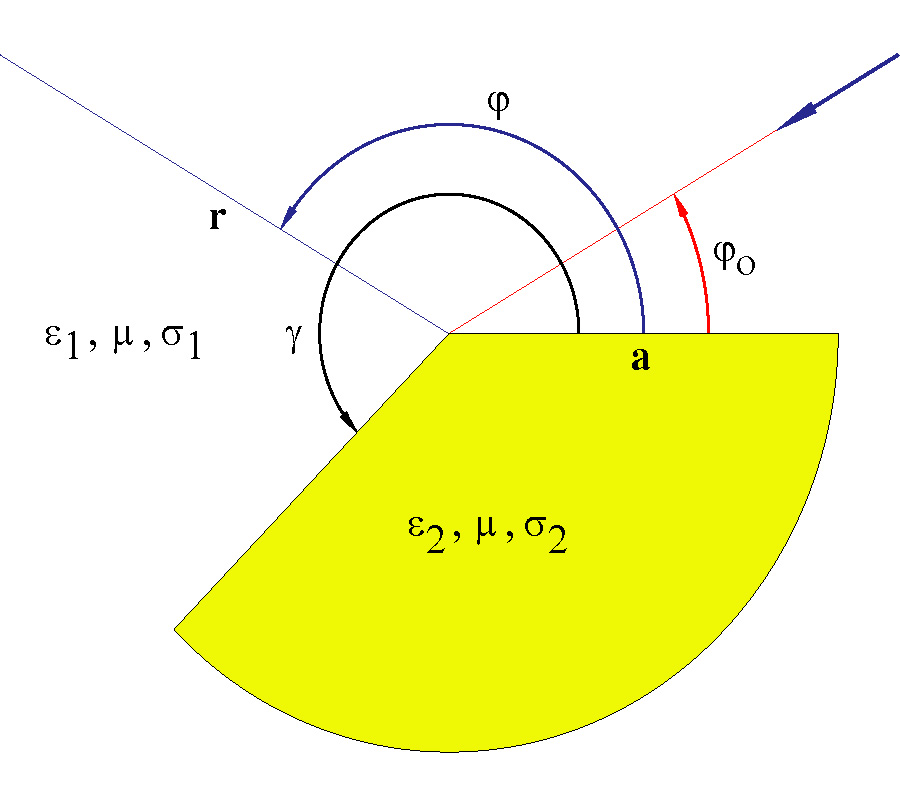
We provide herein open-form, double series formulae describing the diffraction of electromagnetic waves by a dielectric, dissipative wedge of finite radius a: Our procedure bypasses altogether any attempt to enforce boundary conditions at wedge faces, and relies instead on volume self-consistency for the total electric field, incident plus self-consistently radiated by polarization/ohmic currents distributed throughout the wedge interior. Self-consistency of this sort is formulated as an integral equation over the wedge cross-sectional area, an equation wherein are implicitly subsumed all necessary boundary conditions. The crux of the ensuing solution depends upon a decomposition within the wedge interior of both incoming (here taken as plane) wave field and the underlying Green's (Hankel) function into standard functional buildings blocks individually compliant with the Helmholtz equation as adapted to the reference, exterior medium. With such decomposition in hand, the remainder of the solution follows a more or less routine, Ewald-Oseen route, one eased by function orthogonality, by cancellation across the board of the total field when similarly so decomposed throughout the wedge interior, and an almost rote reading off of interior expansion coefficients against those found on the exterior. The incoming field series decomposition across the wedge interior, it should be noted, avoids the pitfall of a naive recourse to Fourier series, and invokes instead a root-mean-square minimization. That such a procedure enjoys a measure of validity is confirmed in Appendix C, wherein it is shown that the present analytic apparatus, when permitted to confront a degenerate wedge having its exterior angle γ tending to zero, γ→0+; which is to say, a bona fide dielectric cylinder, recovers the classical, boundary-value solution as to its every detail. All in all, while we do hope that the present work will serve to broaden the prevailing viewpoint as to permeable wedge scattering, we nevertheless admit to a measure of regret as to the complexity of the resulting formulae, whose numerical implementation bodes ominously to be a formidable task in its own right. It would seem that we reach here a frontier of diminishing returns as to the applications of classical analysis, a point at which its intellectual allure can honorably surrender to direct, computer-driven point matching methods.