PIER | PIER Journals

2024-12-27

PIER

Vol. 181, 99-112, 2024

download: 53

Three-Dimensional Topological Photonic Crystals (Invited Review)

Jian-Wei Liu, Gui-Geng Liu and Baile Zhang

Photonic crystals, often referred to as the ``semiconductors of light,'' have entered a new phase enabling exotic properties once exclusive to topological quantum matter such as topological insulators. While the development of the first three-dimensional (3D) photonic crystal marked the establishment of photonic crystals as an independent field, initial studies in topological photonic crystals focused mainly on one and two dimensions. Though a true photonic crystal counterpart of a 3D strong topological insulator remains elusive, significant progress has been made toward achieving 3D topological photonic crystals. Compared with their lower-dimensional counterparts, 3D topological photonic crystals reveal a richer variety of topological phases and surface manifestation, which enables more degrees of freedom for light manipulation. In this review, concentrating on the novel boundary states unique in 3D systems, we provide a brief survey of the 3D topological photonic crystals and recent advances in this field. We categorize and discuss various topological phases and associated phenomena observed in 3D photonic crystals, including both gapped and gapless phases. Additionally, we delve into some recent developments in this rapidly evolving area, including the realization of 3D topological phases through synthetic dimensions.

Three-dimensional Topological Photonic Crystals (Invited Review)

2024-12-21

PIER

Vol. 181, 35-41, 2024

doi:10.2528/PIER24120802

download: 154

Observation of Polarization-Maintaining Near-Field Directionality

Tong Cai, Yuhan Zhong, Dan Liu, Hailin Huang, Dengpan Wang, Yi Yang, Hongsheng Chen and Xiao Lin

Directional and highly-efficient excitation of guided waves is closely related to the on-chip information processing and is of fundamental importance to plasmonics, nanophotonics, and chiral quantum optics. However, during the directional coupling between propagating waves and guided waves, there is a loss of information about the incident polarization state. It remains elusive and challenging to preserve the incident polarization information in the near-field directionality. Here we experimentally demonstrate polarization-maintaining and polarization-dependent near-field directionality at a microwave frequency of 9.5 GHz by exploiting a reflection-free, anisotropic, and gradient metasurface. The s- and p-polarized guided waves are excited only by the s- and p-polarized components of incident waves, respectively, and they propagate predominantly to opposite designated directions. Remarkably, the measured coupling efficiency between propagating waves and guided waves exceeds 85% for arbitrary incident polarization states. Our work thus reveals a promising route to directly and efficiently convert the polarization-encoded photon qubits to polarization-encoded guided waves, a process that is highly sought after in the context of optical network and plasmonic circuitry.

Observation of Polarization-maintaining Near-field Directionality

2024-12-21

PIER

Vol. 181, 21-33, 2024

doi:10.2528/PIER24111901

download: 142

Dual Non-Diffractive Beam Generation via Spin-and-Frequency Multiplexed All-Dielectric Metasurfaces

Chunyu Liu, Yanfeng Li, Fan Huang, Guanghong Xu, Quan Li, Shuang Wang, Quan Xu, Jianqiang Gu and Jiaguang Han

Metasurfaces offer remarkable capabilities for manipulating electromagnetic waves and by incorporating multiplexing techniques can significantly increase the versatility of design possibilities. Here, we designed and experimentally demonstrated a series of dual non-diffractive beam generators for terahertz radiation based on all-dielectric metasurfaces. These generators could produce switchable Bessel beams and abruptly autofocusing beams depending on the spin and frequency of the incident terahertz waves. In addition, by further applying appropriate phase gradients in the design, these non-diffractive beams could be deflected in specified directions. It is also possible to simultaneously generate multiple non-diffractive beams with different properties. The generated non-diffractive beams were measured with near-field scanning terahertz microscopy, and the results agreed well with simulations. We believe that these metasurface-based beam generators hold tremendous potential in terahertz imaging, communications, non-destructive evaluation, and many other applications.

$Dual Non-diffractive Beam Generation via Spin-and-frequency Multiplexed All-dielectric Metasurfaces$

2024-12-20

PIER

Vol. 181, 1-8, 2024

doi:10.2528/PIER24120305

download: 147

Reflectionless Refraction via One-Dimensional Ghost Polaritons in Planar Junctions of Hyperbolic Metasurfaces

Zhiwei He, Huaping Wang, Zhenyang Cui, Sihao Xia, Xingyu Tang, Bin Zheng, Xiao Lin, Lian Shen, Hongsheng Chen and Yingjie Wu

Polaritons, part-light−part-matter waves, enable the control of light at the subwavelength scale. Interfacial behaviors play a critical role in polariton manipulation, with negative refraction showing promise for high-resolution focusing. However, reflections pose a substantial challenge, especially in applications where backscattering is unwanted. To address this issue, we propose a structure composed of planar junctions of metasurfaces, each supporting in-plane hyperbolic polaritons with misaligned optical axes. We demonstrate that when the asymptote of the incident hyperbolic isofrequency contours (IFCs) aligns with the interface normal, the reflected waves transform into highly lossy one-dimensional ghost polaritons (HL-1DGPs), channeling energy near the interface. The refracted waves also convert into HL-1DGPs when the outgoing IFC asymptote aligns with the interface normal. Leveraging these phenomena, we design polaritonic lenses and absorbers with greatly reduced reflection. These insights into the interfacial behaviors of hyperbolic polaritons under symmetry breaking have implications for creating polaritonic elements beyond the diffraction limit.

$Reflectionless Refraction via One-dimensional Ghost Polaritons in Planar Junctions of Hyperbolic Metasurfaces$

2024-12-25

PIER

Vol. 181, 81-87, 2024

doi:10.2528/PIER24121102

download: 80

Dual-Color Self-Synchronized Cross-Phase-Modulation Mode-Locked Fiber Laser for Coherent Anti-Stokes Raman Scattering Detection

Pu Sun, Haolin Yang, Xiaer Zou, Ke Feng, Ruili Zhang and Sailing He

We present a self-synchronized dual-color cross-phase-modulation mode-locked (XPM ML) fiber laser with excellent wavelength tunability and signal-to-noise ratio for coherent anti-Stokes Raman scattering (CARS) detection. Cross-phase-modulation gives rise to self-synchronization between the two-color lasers, which enables rapid wavelengths scanning as time delay of the master laser cavity is electrically adjusted. The synchronized cavity without any mode-locking elements helps to improve the mode-locking stability and resistance to environmental interference. The pump (780 nm, 18.5 ps) and Stokes (881.1-899.4 nm, 1.5 ps) pulses obtained by second harmonic generation (SHG) are then sent to a focusing lens for CARS detection for scanning Raman shift of 1470-1701 cm^-1). As an example of analyte, rhodium-bisphosphine complex catalyst samples are detected. This highly stable and fast-tunable two-color XPM synchronized mode-locked laser architecture has the potential for arbitrary waveband extension would greatly improve the possibility of coherent Raman scattering imaging technology from the laboratory to practical applications in e.g. biomedical detection.

Dual-color Self-synchronized Cross-phase-modulation Mode-locked Fiber Laser for Coherent Anti-stokes Raman Scattering Detection

2024-12-23

PIER

Vol. 181, 73-80, 2024

doi:10.2528/PIER24121305

download: 81

Dual-Modal Fluorescent Hyperspectral Micro-CT for Precise Bioimaging Detection

Jing Luo, He Zhu, Raheel Ahmed Janjua, Wenbin Ji, Ruili Zhang, Junbo Liang and Sailing He

In this study, we introduce a dual-modal fluorescence hyperspectral micro-CT system developed for e.g. bioimaging applications. The system integrates an X-ray computed tomography (CT) module with a custom-designed hyperspectral fluorescence imaging module, achieving high-resolution structural imaging with detailed molecular-level insights. With a spectral resolution of 10 nm across the wavelength range of 450–750 nm, the hyperspectral fluorescence imaging module enables a fine compositional analysis. Using surface-modified nanoparticles, we demonstrate the system's capability to capture fluorescence under both X-ray and UV excitation. Imaging experiments on a mouse model further highlight the system's ability to generate comprehensive Four-dimensional (4D) datasets that integrate spatial, spectral, and structural information. To the best of our knowledge, no such a dual-modal system or the like has even been reported before. This dual-modal approach enhances the visualization and analysis of biological tissues, offering promising applications in e.g. disease diagnosis, surgical guidance, and preclinical research.

Dual-modal Fluorescent Hyperspectral Micro-CT for Precise Bioimaging Detection

2024-12-21

PIER

Vol. 181, 9-19, 2024

doi:10.2528/PIER24120505

download: 108

Smartphone-Integrated YOLOv4 -CNN Approach for Rapid and Accurate Point-of-Care Colorimetric Antioxidant Testing in Saliva

Youssef Amin, Paola Cecere, Tania Pomili and Pier Paolo Pompa

This study introduces a machine learning (ML)-based method for point-of-care (POC) colorimetric testing of total antioxidant concentration (TAC) in saliva, an important biomarker for health monitoring. The approach leverages ML to accurately classify color intensity in the POC test. Saliva samples were collected and imaged at specific intervals during the colorimetric reaction, generating a dataset representative of various antioxidant levels. Four classifiers (Convolutional Neural Network, Support Vector Machine, K-Nearest Neighbors, and Single-layer Feed-Forward Neural Network) were evaluated on distinct datasets, with Convolutional Neural Network (CNN) consistently achieving superior performance. To enhance classification accuracy, stacking-based ensemble learning was applied, combining CNN predictions with a Support Vector Machine (SVM) meta-classifier, achieving up to 92% accuracy. Additionally, YOLOv4-tiny was utilized for object detection to isolate regions of interest in the images, creating a refined dataset that a CNN model is then classified with ca. 98% accuracy. This YOLOv4-CNN approach not only improved accuracy but also simplified the model architecture. The integrated object detection and CNN models were deployed on an Android application, enabling real-time TAC analysis on a smartphone with 98% accuracy and a fast readout time of 2 minutes. This method offers a robust, efficient, and accessible solution for POC antioxidant testing.

Smartphone-integrated YOLOv4-CNN Approach for Rapid and Accurate Point-of-Care Colorimetric Antioxidant Testing in Saliva

2024-12-27

PIER

Vol. 181, 89-98, 2024

doi:10.2528/PIER24120903

download: 50

An Indoor Localization Technique Utilizing Passive Tags and 3-d Microwave Passive Radar Imaging

Quanfeng Wang, Alexander H. Paulus, Mei Song Tong and Thomas F. Eibert

A privacy-compliant indoor localization approach utilizing a 3-D near-field (NF) passive radar imaging technique is presented. This technique leverages ubiquitously radiated electromagnetic fields for imaging, with passive tags introduced to enhance the strength of scattering fields, thereby enabling precise localization at the imaging level. The method also supports localization in non-ideal imaging scenarios, such as for limited bandwidth or in highly-reflective environments. Based on their geometrical properties the simple and low-cost passive tags enable intuitive differentiation between individuals or objects. Associated privacy protection mechanisms are discussed, where the frequency-varying properties of the passive tags provide additional flexibility and potential applications under privacy and ethical considerations. Several forms of passive tags are presented, where both simulation and experimental results validate the effectiveness of the proposed passive tag designs.

An Indoor Localization Technique Utilizing Passive Tags and 3-D Microwave Passive Radar Imaging

2024-12-23

PIER

Vol. 181, 61-72, 2024

doi:10.2528/PIER24112606

download: 112

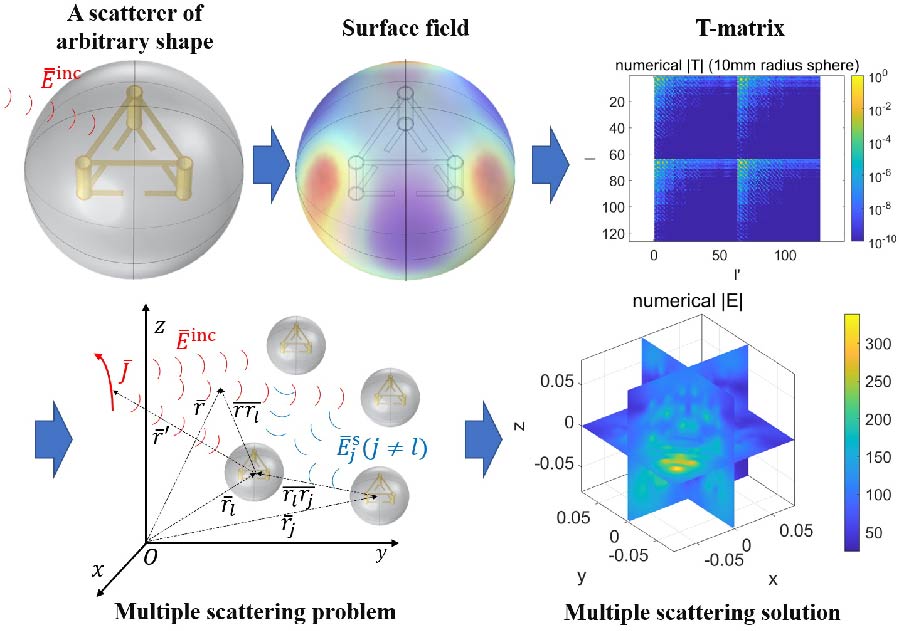
An Efficient Hybrid Numerical T-Matrix Approach for 3D Multiple Scattering Analysis

Haifeng Zheng, Xuyang Bai, Shurun Tan and Leung Tsang

In the past decades, with the increasing complexity of topological crystals, artificial electromagnetic (EM) materials, and EM environments, understanding their precise scattering behaviors and characteristis is turning more challenging. Traditional methods for modeling these properties often rely on full-wave simulations or analytical algorithms which are only applicable for regular shapes with plane wave incidences. These methods are inefficient for the design and broadband multiple scattering analysis of general 3D EM structures, as new simulations are required for each different scattering scenario and frequency, while solving a substantial number of unknown variables in each analysis. In this paper, a novel hybrid numerical scattering T-matrix extraction method applicable to scatterers of arbitrary shape and composition is developed in the context of the Foldy-Lax multiple scattering theory (F-L MST). Generalization is also made such that the F-L MST can be applied to multiple scattering problems with arbitrary incident fields. Once the T-matrix elements of individual scatterers are obtained through combining spherical wave expansion with full-wave numerical simulations of surface fields as proposed in the paper, it can be stored and reused, significantly reducing the overall computational complexity. Compared to conventional methods, this approach merely requires matrix inversions of moderate orders in a multiple scattering problem, offering notable efficiency advantages for about an order of magnitude. Meanwhile, the smooth frequency dependence of the T-matrix elements and incident field coefficients suggests the feasibility of interpolating these coefficients for broadband simulations. This proves particularly helpful in the swiftly evolving near-field techniques, and scenarios requiring extensive analysis such as broadband and Monte Carlo analysis. Numerical cases, involving multiple scatterer shapes and arrangements, are explored and compared with COMSOL full-wave simulations. The results validate the accuracy and efficiency of the proposed method, with potential to become a powerful tool for EM simulations and optimization of various wave-functional materials and in many other multiple scattering applications.

An Efficient Hybrid Numerical T-matrix Approach for 3D Multiple Scattering Analysis

2024-12-22

PIER

Vol. 181, 43-59, 2024

doi:10.2528/PIER24110103

download: 68

(3+1)-Dimensional Nonparaxial Spatiotemporally Localized Waves in Transparent Dispersive Media

Ioannis Besieris

Most of the analytical work on general transparent dispersive media to date has been confined to second-order dispersion within the framework of the paraxial approximation. It is the aim in this article to lift this restriction. Specifically, a detailed discussion is provided of modulated (3+1)-dimensional nonparaxial spatiotemporally localized waves in second-order transparent dispersive media. Novel infinite-energy invariant wavepackets and finite-energy almost undistorted solutions are discussed in detail. Illustrative numerical examples of the latter are given for normal dispersion in fused silica and for anomalous dispersion in a Lorentz plasma.