PIER | PIER Journals

2020-08-23

PIER

Vol. 167, 111-126, 2020

doi:10.2528/PIER20030601

download: 392

A Combined Active and Passive Method for the Remote Sensing of Ice Sheet Temperature Profiles

Haokui Xu , Leung Tsang , Joel Johnson , Kenneth C. Jezek , Jie-Bang Yan and Prasad Gogineni

The Ultra-Wideband Software defined microwave radiometer (UWBRAD) was developed to probe internal ice sheet temperatures using 0.5-2 GHz microwave radiometry. The airborne brightness temperature data of UWBRAD show a significant reduction due to reflections of surface layering of density fluctuations making difficult the retrieval of subsurface temperature in the kilometer range of depth. Such reflections can be measured by the ultra-wideband radar in the same frequency range suggesting a combined active and passive remote sensing of polar ice sheets. In this paper, we develop a coherent reflectivity model for both ice sheet thermal emission and backscattering. Maxwell equations are used to calculate the coherent reflections from the cap layers, and the WKB approximation is used to calculate the transmission for the slowly varying profile below the cap layers. Results are then shown to demonstrate the use of radar measurements to compensate reflection effects on brightness temperatures. It is shown that the reflections corrected brightness temperature is directly related to the physical temperature and absorption profile making possible the retrieval of subsurface temperature profile with multi-frequency measurements

A COMBINED ACTIVE AND PASSIVE METHOD FOR THE REMOTE SENSING OF ICE SHEET TEMPERATURE PROFILES

2020-07-09

PIER

Vol. 167, 95-109, 2020

doi:10.2528/PIER20041601

download: 465

Investigation of New Sectored Hemispherical Dielectric Resonator Antennas Operating at TM₁₀₁ and TE₁₁₁ Mode for Circular Polarization

Rakesh Chowdhury and Raghvendra Kumar Chaudhary

This article discusses the effect of sectorization technique in hemispherical dielectric resonator antennas (HDRA) for the first time with its significant effects on electromagnetic modes and various antenna parameters. The sector angle (β) forms an additional framework for better optimization of HDRA. The resonance frequency, impedance bandwidth, co-cross polarization characteristics have been investigated in new sectored HDRA geometries excited at their TE₁₁₁ and TM₁₀₁ modes. Further, examination of circular polarization (CP) is carried out by detuning of degenerate orthogonal modes in HDRAs, and β = 180° has been particularly examined in details for CP. Based on the results, appropriate values of `β' and probe position (P_r) are chosen followed by modelling a prototype and experimental.

INVESTIGATION OF NEW SECTORED HEMISPHERICAL DIELECTRIC RESONATOR ANTENNAS OPERATING AT TM<sub>101</sub> AND TE<sub>111</sub> MODE FOR CIRCULAR POLARIZATION

2020-07-07

PIER

Vol. 167, 83-94, 2020

doi:10.2528/PIER20040201

download: 901

Shark-Fin Antenna for Railway Communications in LTE-R, LTE, and Lower 5G Frequency Bands

Ashwini Kumar Arya , Seong Jin Kim , Sungik Park , Dong-Hoon Kim , Rehab S. Hassan , Kyeongjun Ko and Sanghoek Kim

This paper presents a design study of a shark-fin antenna for future railway communications. Three specific bands are considered here as LTE-R (700 MHz), LTE (2100 MHz), and Lower 5G Band (3500 MHz). A 3-D metallic structure using the 3D printing technique has been designed and fabricated for the consideration of the required bands. The size (volume) of the antenna element is 163 × 61.9 × 10 mm³. The multi-physical simulations in terms of the smooth air flow and lower drag coefficient are performed for analyzing the need of shark-fin radome cover. More than 70 MHz bandwidth was observed for the LTE-R band and also a wide band response was observed that cover the required bands well i.e. the LTE, and lower 5G band. The proposed shark-fin antenna results the expected ideal radiation performance with an omnidirectional behavior in the horizontal plane.

SHARK-FIN ANTENNA FOR RAILWAY COMMUNICATIONS IN LTE-R, LTE, AND LOWER 5G FREQUENCY BANDS

2020-06-29

PIER

Vol. 167, 67-81, 2020

doi:10.2528/PIER20030705

download: 2188

A Review of Deep Learning Approaches for Inverse Scattering Problems (Invited Review)

Xudong Chen , Zhun Wei , Maokun Li and Paolo Rocca

In recent years, deep learning (DL) is becoming an increasingly important tool for solving inverse scattering problems (ISPs). This paper reviews methods, promises, and pitfalls of deep learning as applied to ISPs. More specifically, we review several state-of-the-art methods of solving ISPs with DL, and we also offer some insights on how to combine neural networks with the knowledge of the underlying physics as well as traditional non-learning techniques. Despite the successes, DL also has its own challenges and limitations in solving ISPs. These fundamental questions are discussed, and possible suitable future research directions and countermeasures will be suggested.

A REVIEW OF DEEP LEARNING APPROACHES FOR INVERSE SCATTERING PROBLEMS (INVITED REVIEW)

2020-05-31

PIER

Vol. 167, 55-65, 2020

doi:10.2528/PIER20012102

download: 410

Design and Fabrication of a Sectoral Beam Slotted Antenna in SIW Technology for Surveillance Applications at Millimeter Waves

Santi Concetto Pavone and Matteo Albani

In this paper, we present the design and fabrication of a sectoral beam slotted antenna in substrate integrated waveguide (SIW) technology able to achieve a high roll-off sectoral pattern in the horizontal plane and a very narrow beam in the vertical plane, as required in surveillance applications in the band 76-77 GHz. The proposed antenna is designed and fabricated in multi-layer PCB technology, which allows to integrate both the corporate feeding network and the radiating aperture in the same planar and lightweight device. To achieve a remarkable roll-off (> 5.5 dB/deg) and a reduced ripple (< 1.5 dB), the antenna has been designed by synthesizing a sinc-shaped (uniform) aperture distribution along x-direction (y-direction). The synthesis and optimization of so tapered aperture distributions is not easy to be found in the literature, especially for planar devices. A prototype of such an antenna has been fabricated with a horizontal half-power beamwidth (HPBW) of 30˚, by embedding both the feeding network and the radiating aperture in three stacked dielectric substrates. Measurements of the prototype show a fair agreement with numerical simulations.

DESIGN AND FABRICATION OF A SECTORAL BEAM SLOTTED ANTENNA IN SIW TECHNOLOGY FOR SURVEILLANCE APPLICATIONS AT MILLIMETER WAVES

2020-03-19

PIER

Vol. 167, 41-54, 2020

doi:10.2528/PIER20031008

download: 375

Self-Dual Boundary Conditions in Electromagnetics

Ismo Veikko Lindell and Ari Sihvola

Invariance in duality transformation, the self-dual property, has important applications in electromagnetic engineering. In the present paper, the problem of most general linear and local boundary conditions with self-dual property is studied. Expressing the boundary conditions in terms of a generalized impedance dyadic, the self-dual boundaries fall in two sets depending on symmetry or antisymmetry of the impedance dyadic. Previously known cases are found to appear as special cases of the general theory. Plane-wave reflection from boundaries defined by each of the two cases of self-dual conditions are analyzed and waves matched to the corresponding boundaries are determined. As a numerical example, reflection from a special case, the self-dual EH boundary, is computed for two planes of incidence.

SELF-DUAL BOUNDARY CONDITIONS IN ELECTROMAGNETICS

2020-03-15

PIER

Vol. 167, 31-39, 2020

doi:10.2528/PIER19121807

download: 402

One-Antenna Radiation Pattern Measurement of on-Wafer Antennas in Probe Station Environment

Jianfang Zheng , Juha Ala-Laurinaho , Zachary D. Taylor and Antti V. Räisänen

We propose and demonstrate the use of radiation pattern measurement method for on-wafer antennas for the first time that is capable of in-depth antenna characterization with limited equipment. This one-antenna method extracts gain without the need for a second antenna in the on-wafer probe station environment. A combination of reference reflector translation and rotation allows radiation pattern sampling at multiple angles enabling characterization over the relevant solid angle. Several microstrip patch antennas with varying beam directions (0˚, 20˚, and 30˚) were measured with the proposed method over 120˚ in the H-plane with good agreement between simulation and experiment. The method offers a cost-effective and time-efficient solution for probe-fed, on-wafer antenna radiation performance characterization.

ONE-ANTENNA RADIATION PATTERN MEASUREMENT OF ON-WAFER ANTENNAS IN PROBE STATION ENVIRONMENT

2020-02-23

PIER

Vol. 167, 19-30, 2020

doi:10.2528/PIER19112609

download: 604

Multi-Objective Genetic Algorithm Optimization of Frequency Selective Metasurfaces to Engineer Ku-Passband Filter Responses

Kenneth W. Allen , Daniel J. P. Dykes , David R. Reid and Richard Todd Lee

Metasurfaces enable a new avenue to create electrically thin multi-layer structures, on the order of one-tenth the central wavelength (λ_c), with engineered responses. Altering the sub-wavelength spatial features, e.g. λ_c/80, on the surface leads to highly tunable electromagnetic scattering characteristics. In this work, we develop an ultra-wideband frequency selective metasurface (FSmS) that completely encompasses the Ku-band from 12-18 GHz with steep band edges. The geometrical structure of the metasurfaces is optimized by a multi-objective genetic algorithm mimicking evolutionary processes. Analysis is performed from one- to four-layer metasurface structures with various thicknesses. Computational electromagnetic simulations for these frequency selective metasurfaces (FSmS) are presented and discussed. The concepts presented in this work can be applied to design metasurfaces and metamaterials from the microwave to the optical regimes.

MULTI-OBJECTIVE GENETIC ALGORITHM OPTIMIZATION OF FREQUENCY SELECTIVE METASURFACES TO ENGINEER KU-PASSBAND FILTER RESPONSES

2020-02-17

PIER

Vol. 167, 11-17, 2020

doi:10.2528/PIER20011301

download: 353

Generating Picosecond Pulses with the Largest Number of Lasing Wavelengths by an All-Fiber Optical Parametric Oscillator

Xiaogang Jiang , Feihong Chen , Yi Lu , Taoce Yin and Sailing He

An all-fiber parametric oscillator which is pumped by a mode-locked Er-doped picosecond fiber laser is proposed for the generation of multi-wavelength picosecond lasing pulses. The length of a fiber-coupled optical delay line is adjusted so that the first signal wavelength is tuned closer to the pump wavelength to facilitate the generation of more lasing wavelengths. 10 orders of cascaded four-wave-mixing processes are achieved and picosecond pulses at 17 lasing wavelengths from 1264.7 nm to 1842.4 nm are demonstrated. To the best of our knowledge, this is the largest number of lasing wavelengths reported so far from a fiber optical parametric oscillator pumped with an ultrashort-pulse laser.

GENERATING PICOSECOND PULSES WITH THE LARGEST NUMBER OF LASING WAVELENGTHS BY AN ALL-FIBER OPTICAL PARAMETRIC OSCILLATOR

2020-01-18

PIER

Vol. 167, 1-10, 2020

doi:10.2528/PIER19090908

download: 385

Shielding of an Imperfect Metallic Thin Circular Disk: Exact and Low-Frequency Analytical Solution

Giampiero Lovat , Paolo Burghignoli , Rodolfo Araneo , Salvatore Celozzi , Amedeo Andreotti , Dario Assante and Luigi Verolino

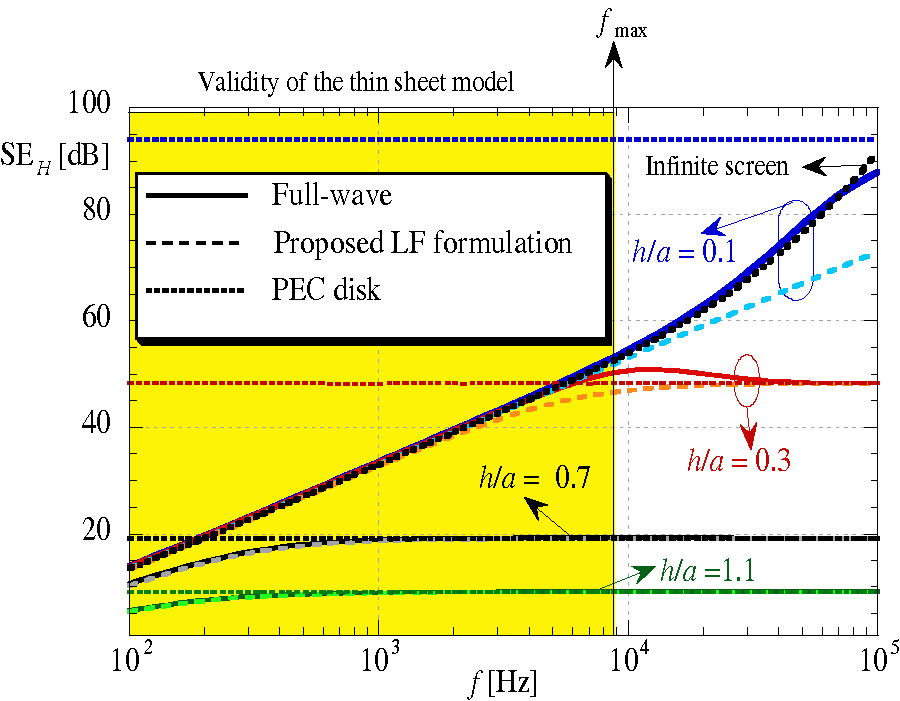
The problem of evaluating the shielding effectiveness of a thin metallic circular disk with finite conductivity against an axially symmetric vertical magnetic dipole is addressed. First, the thin metallic disk is modeled through an appropriate boundary condition, and then, as for the perfectly conducting counterpart, the problem is reduced to a set of dual integral equations which are solved in an exact form through the application of the Galerkin method in the Hankel transform domain. A second-kind Fredholm infinite matrix-operator equation is obtained by selecting a suitable set of basis functions. A low-frequency solution is finally extracted in a closed form. Through a comparison with results obtained from a full-wave commercial software, it is shown that such a simple approximate solution is accurate up to the frequency where the surface-impedance model of the thin disk is valid.