The Three Exact Components of the Magnetic Field Created by a Radially Magnetized Tile Permanent Magnet
Romain Ravaud,
Guy Lemarquand,
Valerie Lemarquand and
Claude Depollier
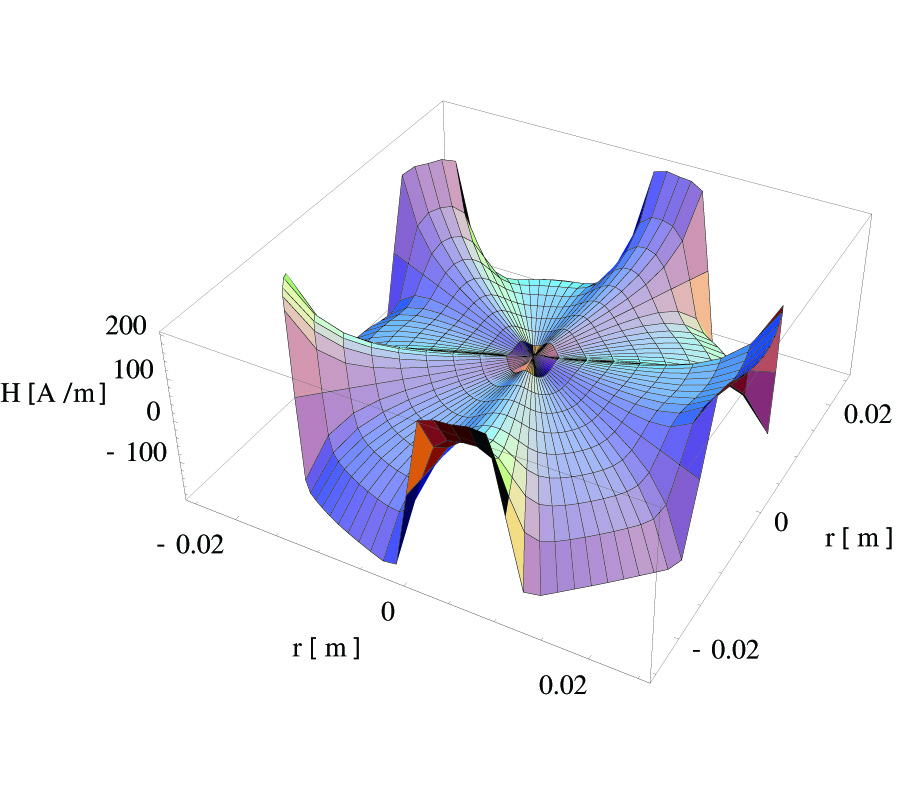
This paper presents the exact analytical formulation of the three components of the magnetic field created by a radially magnetized tile permanent magnet. These expressions take both the magnetic pole surface densities and the magnetic pole volume density into account. So, this means that the tile magnet curvature is completely taken into account. Moreover, the magnetic field can be calculated exactly in any point of the space, should it be outside the tile magnet or inside it. Consequently, we have obtained an accurate 3D magnetic field as no simplifying assumptions have been used for calculating these three magnetic components. Thus, this result is really interesting. Furthermore, the azimuthal component of the field can be determined without any special functions. In consequence, its computational cost is very low which is useful for optimization purposes. Besides, all the other expressions obtained are based on elliptic functions or special functions whose numerical calculation is fast and robust and this allows us to realize parametric studies easily. Eventually, we show the interest of this formulation by applying it to one example: the calculation and the optimization of alternate magnetization magnet devices. Such devices are commonly used in various application fields: sensors, motors, couplings, etc. The point is that the total field is calculated by using the superposition theorem and summing the contribution to the field of each tile magnet in any point of the space. This approach is a good alternative to a finite element method because the calculation of the magnetic field is done without any simplifying assumption.