Analytical Techniques to Evaluate the Integrals of 3D and 2D Spatial Dyadic Green's Functions
Guozhong Gao
,
Carlos Torres-Verdin
and
Tarek Habashy
The Dyadic Green's function is in general viewed as a generalized, or distribution function. A commonly used procedure to evaluate its volume integral is the principal-volume method, in which an infinitesimal volume around the singularity is excluded from the integration volume. In this paper, we develop a general analytical technique to evaluate the integral of the dyadic Green's function without the need to specify an exclusion volume.
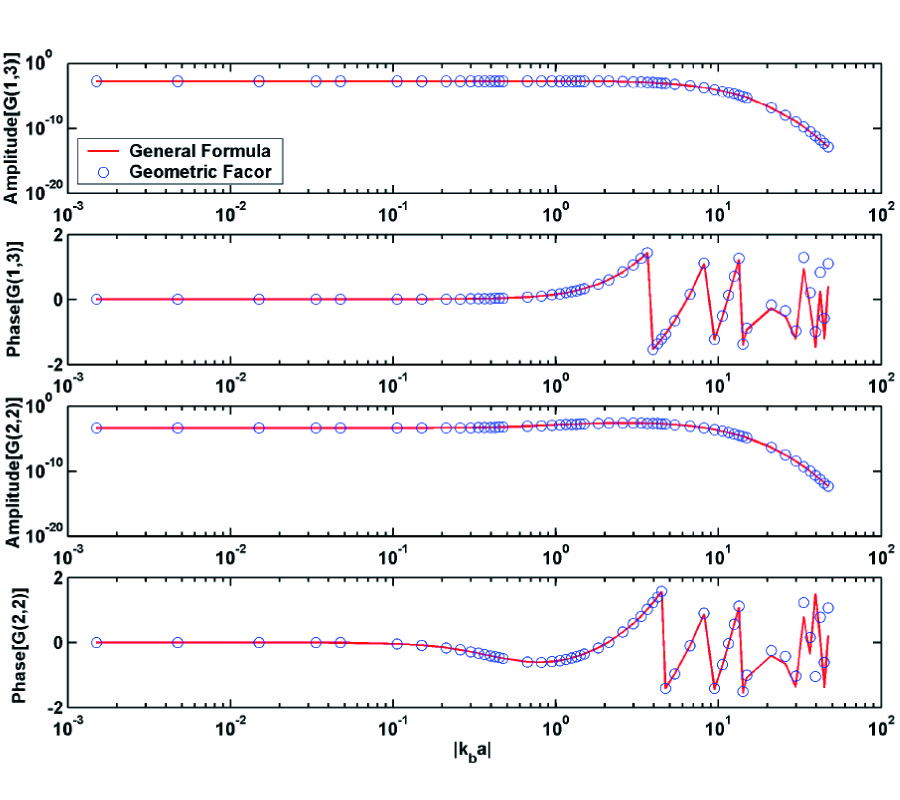
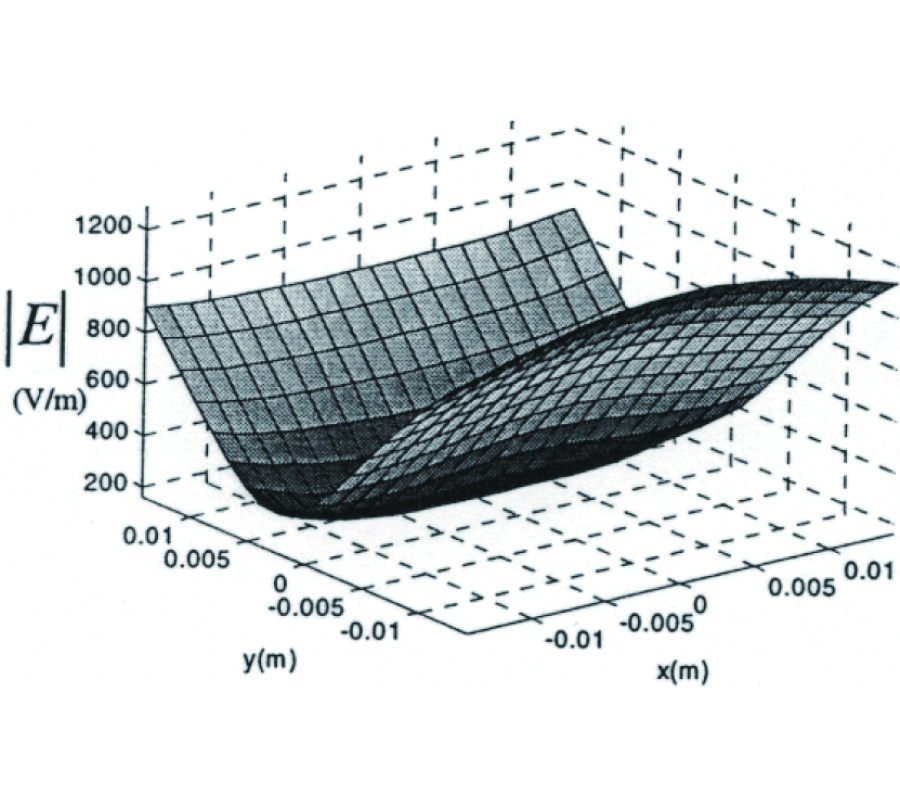
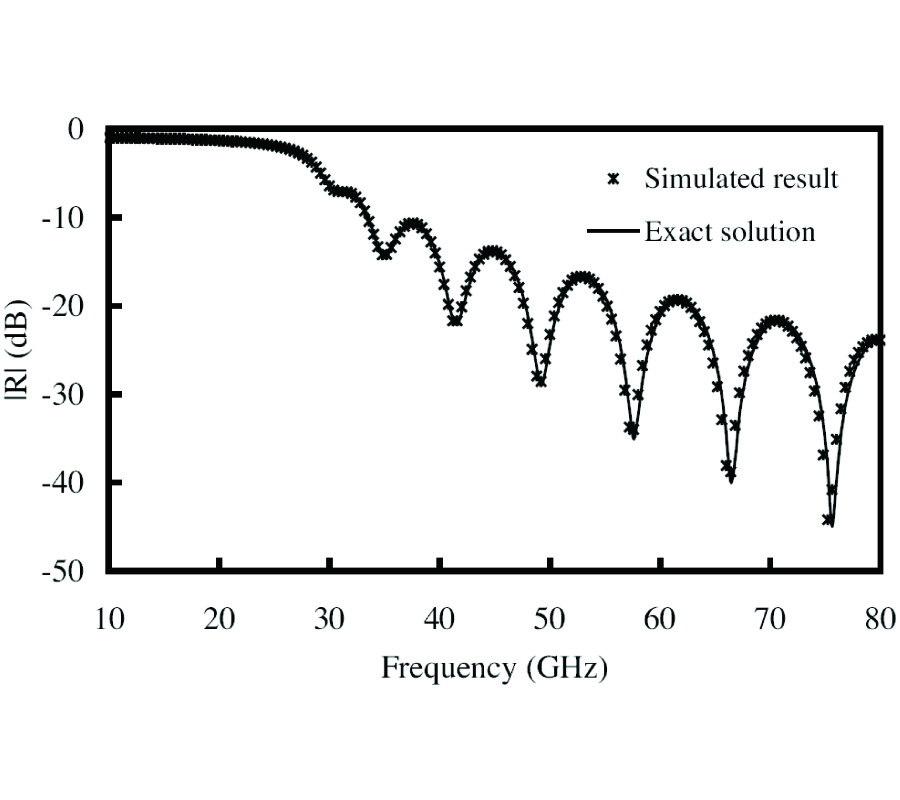
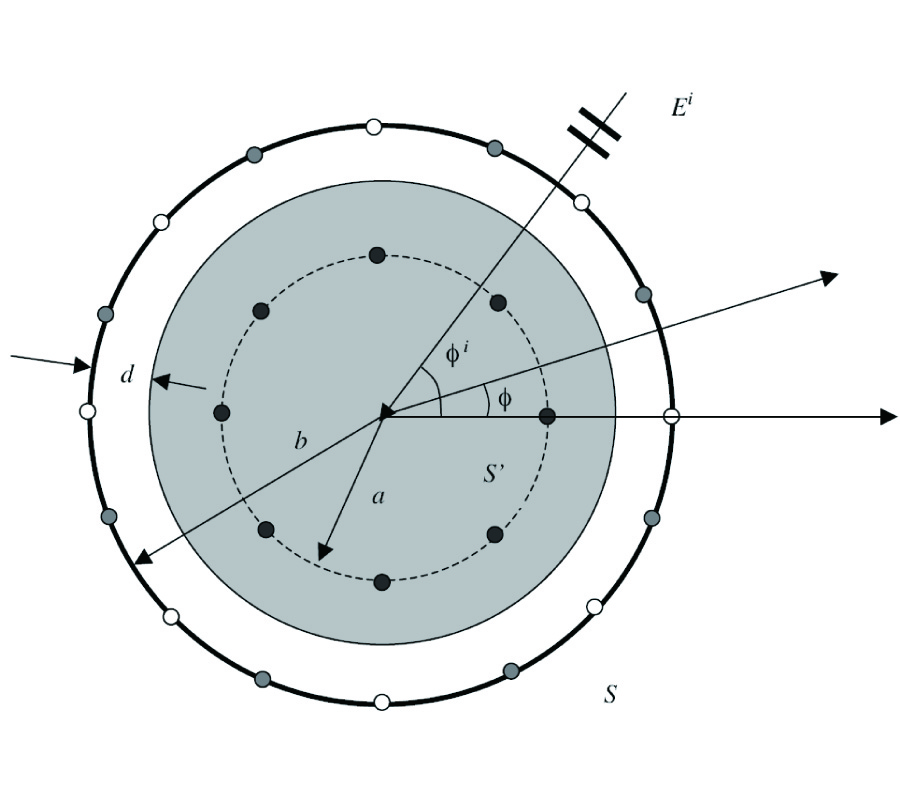
The newly derived expressions accurately integrate the singularity and can be used for integration over any shape of spatial discretization cell. We derive explicit expressions for the integral of the 3D dyadic Green's function over a sphere and over a general rectangular block. Similar expressions are obtained for the 2D dyadic Green's function over a cylinder and over a general rectangular cell. It is shown that using the integration technique described in this paper for spherical/circular cells, simple analytical expressions can be derived, and these expressions are exactly the same as those obtained using the principal-volume method. Furthermore, the analytical expressions for the integral of the dyadic Green's function are valid regardless of the location of the observation point, both inside and outside the integration domain. Because the expressions only involve surface integrals/line integrals, their evaluation can be performed very efficiently with a high degree of accuracy. We compare our expressions against the equivalent volume approximation for a wide range of frequencies and cell sizes. These comparisons clearly show the efficiency and accuracy of our technique.
It is also shown that the cubic cell (3D) and the square cell (2D) can be approximated with an equivalent spherical cell and circular cell, respectively, over a wide range of frequencies. The approximation can be performed analytically, and the results can be written as the value of the dyadic Green's function at the center multiplying a "geometric factor". We describe analytical procedures to derive the corresponding geometric factors.