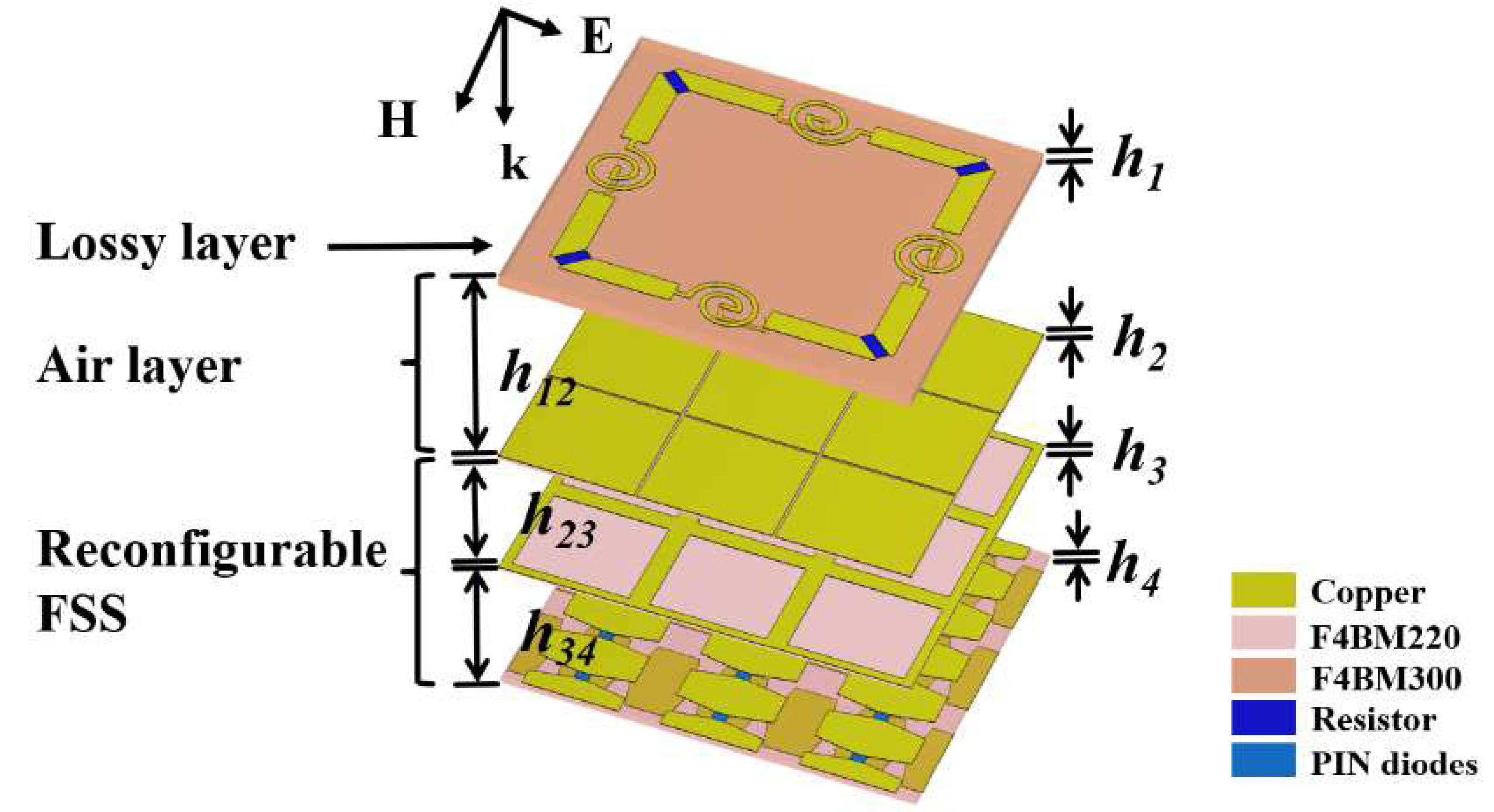
Design of an Efficient SRR Loaded Polarization-Independent Wideband Metamaterial Notched Absorber with Wide Reflecting Band for Low Insertion Loss
Abhinav Kumar and
Jayanta Ghosh
This research introduces a new, compact, absorptive frequency-selective reflector, or notched absorber (AFSR), which is low-profile and polarization-insensitive. The objective of the proposed study is to create a miniaturized FSS-based notched absorber that exhibits a high level of angular stability and a robust operational bandwidth of 110% (4.1 to 14.1 GHz). It consists of a reflecting band situated between two absorption bands. The absorption bands are 4.1 to 5.7 GHz and 9.0 to 14.1 GHz, respectively. A low insertion loss of 0.40 dB is achieved at approximately 6.8 GHz, and a wide reflection window with a -3 dB band is extended from 5.8 GHz to 8.0 GHz. The proposed notched absorber comprises three layers with a metal sheet at the bottom. The intermediate layer serves as a bandpass filter, which passes the in-band signal while working as a ground plane for out-of-band absorption. In contrast, the top layer is responsible for broad out-of-band absorption. The total thickness of the band notch absorber is 0.36λ (where λ stands for the wavelength associated with the lowest operating frequency). The equivalent circuit model of the proposed structure has been developed to understand better how band-notch absorbers work at their most basic level. In addition, we examined the distribution of surface current. The notched absorber that was designed is fabricated, and measurements have been done in a semi-anechoic chamber. The measured results are in excellent agreement with the simulated ones. The proposed notched absorber can be employed in radomes, to reduce electromagnetic interference and protect sensitive equipment from unwanted electromagnetic radiation, superstratum on an antenna, RCS reduction and stealth characteristics.